コメント |
|
また福島産米の話かよ。以前、めげ猫は「県検査で 76Bq/kg 以上の誤差がある」なんて言ってたが、これは全くのデマだ。俺の分析結果を書いておくぞ。
■ 「福島産米の全量全袋検査の 1 段目の県検査において 76Bq/kg 以上の誤差がある」という証拠はない。
全量全袋検査に関するスクリーニングレベルの説明
[ http://www.pref.fukushima.lg.jp/sec/36035b/zenryouzenhukurokensa-screeninglevel.html ]
には
「福島県で導入している5種類の検査器では、スクリーニングレベルは、おおむね50〜80Bq/kgの範囲で設定されています。」
とある。スクリーニングレベルは一律に 76Bq/kg に設定されているわけではない。更に「めげ猫」が参照した「報道発表資料|厚生労働省」は
平成29年10月19日公表 [ http://www.pref.fukushima.lg.jp/uploaded/attachment/240652.pdf ]
セシウム-134[Bq/kg] 検出せず(<3.2)
セシウム-137[Bq/kg] 18.6
合算値[Bq/kg] 19
平成29年11月7日公表 [ http://www.pref.fukushima.lg.jp/uploaded/attachment/240651.pdf ]
セシウム-134[Bq/kg] 検出せず(<4.4)
セシウム-137[Bq/kg] 6.18
合算値[Bq/kg] 6.2
平成29年12月5日公表 [ http://www.pref.fukushima.lg.jp/uploaded/attachment/244888.pdf ]
セシウム-134[Bq/kg] 5.07
セシウム-137[Bq/kg] 42.4
合算値[Bq/kg] 47
平成29年12月18日公表 [ http://www.pref.fukushima.lg.jp/uploaded/attachment/246669.pdf ]
セシウム-134[Bq/kg] 検出せず(<4.2)
セシウム-137[Bq/kg] 検出せず(<3.6)
合算値[Bq/kg] 検出せず
の 4 件であるが、これらにはスクリーニングレベルの記載はない。
(続く)
|
|
>>1 (続き)
そもそも「めげ猫」が誤差だと主張している 76Bq/kg は標準偏差でも標準誤差でもないので、放射線の測定ではこの 76Bq/kg を誤差とは呼ばない。また
食品中の放射性セシウムスクリーニング法
[ http://www.mhlw.go.jp/stf/houdou/2r98520000021b3t-att/2r98520000021b8j.pdf ]
には
「測定下限値 25Bq/kg(基準値の1/4)以下であること」
と規定されているので、最低限、セシウム濃度 25Bq/kg の試料をバックグラウンドから識別できればよく、それ未満は保証しなくてもよい。従って、問題になりそうなのは平成29年12月5日公表分の「47Bq/kg」だけだが、これはスクリーニングレベルが 50Bq/kg であったとすれば簡単に説明がつく。これ以外の 3 件「19Bq/kg」「6.2Bq/kg」「検出せず」に関しては、標準偏差や標準誤差で説明するのが困難だが、それ以外の要因、例えば検査器の電気的なノイズ等、は考えられるだろう。
■ 実証機の誤差の推定値は最大で約 6.0Bq/kg である。
では、実際の誤差はどの程度か? メーカーが公表しているデータから見積もってみる。
コンベアで次々放射性セシウム検査はずさんなの?
[ https://togetter.com/li/364153 ]
にある図「実証試験結果 ゲルマニウム検出器との比較」から
実証機
-------------------
Ge半導体検出器 最大 最小 平均値
-------------- ------ ----- ------
18.9 27.6 8.2 17.1
31.2 45.82 20.64 31.64
50.1 60.90 39.70 49.18
67.7 81.10 56.74 69.22
77.7 90.49 66.21 77.26
96.8 112.52 85.17 97.58
112.7 124.40 95.75 109.91
-------------- ------ ----- ------
(続く)
|
|
>>2 (続き)
図「実証試験結果」
[ http://chart.apis.google.com/chart?hl=ja&cht=lxy&chs=500x500&chg=9.09091,7.69231,2,2&chtt=%E5%AE%9F%E8%A8%BC%E8%A9%A6%E9%A8%93%E7%B5%90%E6%9E%9C|(%E5%8D%98%E4%BD%8D:+Bq%2Fkg)&chts=0000FF,20&chxt=x,x,y,y&chxr=0,10,120,10|2,0,130,10&chxp=1,50|3,50&chxl=1:|%E7%8E%84%E7%B1%B3%E3%81%AE%E3%82%BB%E3%82%B7%E3%82%A6%E3%83%A0%E6%BF%83%E5%BA%A6|3:|%E6%B8%AC%E5%AE%9A%E5%80%A4&chxs=1,0000FF,15,0|3,0000FF,15,0&chds=10,120,0,130,10,120,0,130,10,120,0,130&chd=t:18.9,31.2,50.1,67.7,77.7,96.8,112.7|27.6,45.82,60.90,81.10,90.49,112.52,124.40|-1|8.2,20.64,39.70,56.74,66.21,85.17,95.75|-1|17.1,31.64,49.18,69.22,77.26,97.58,109.91&chfd=2,x,0,x|4,x,0,x&chls=0|0|1&chm=E,,0,-1,1|N*f,,0,-1,10,,l:4:4|N*f,,1,-1,10,,l:4:4|o,,2,-1,4|N*f,,2,-1,10,,l:4:4 ]
であり、Ge半導体検出器は(推測だが 2kg マリネリで) 1500 秒の測定を 1 回、実証機は 30kg で 15 秒の測定を 100 回である。
標準正規分布 N(0,1) からの無作為標本 x_1、x_2、…、x_n に対する範囲 R (最大値から最小値を引いた値) の期待値 d_2、標準偏差 d_3 の計算には R の密度関数とその k 次モーメント
(続く)
|
|
>>3 (続き)
f(R,n) = n*(n-1)*∫_[-∞,∞][∫_[x,x+R]φ(t)dt]^(n-2)*φ(x)*φ(x+R)dx
φ(x) = 1/√(2*π)*e^(-x^2/2)
E(R^k) = ∫_[0,∞]R^k*f(R,n)dR
d_2 = E(R)
d_3^2 = Var(R) = E(R^2)-{E(R)}^2
[ http://www.codecogs.com/eq.latex?\\f(R,n)=n(n-1)\int_{-\infty}^\infty\left[\int_x^{x+R}\phi(t)dt\right]^{n-2}\phi(x)\phi(x+R)dx\\\phi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\\E(R^k)=\int_0^\infty%20R^kf(R,n)dR\\d_2=E(R)\\d_3^2=Var(R)=E(R^2)-\{E(R)\}^2 ]
を用いるが、これは一般には数値積分になり、「管理図係数表」として公開されている。しかし n は 25 ほどまでである。そこで n が 100 の時の d_2 の近似値が必要になるが
R管理図σを推定する方法と計算式
[ http://support.minitab.com/ja-jp/minitab/18/help-and-how-to/quality-and-process-improvement/control-charts/how-to/variables-charts-for-subgroups/r-chart/methods-and-formulas/estimating-sigma/ ]
によれば、N の値が 51〜100 の場合の d_2(N) の近似式、N の値が 26〜100 の場合の d_3(N) と d_4(N) の近似式はそれぞれ
(続く)
|
|
>>4 (続き)
d_2(N) = 3.4873+0.0250141*N-0.00009823*N^2
d_3(N) = 0.80818-0.0051871*N+0.00005098*N^2-0.00000019*N^3
d_4(N) = 2.88606+0.051313*N-0.00049243*N^2+0.00000188*N^3
[ http://www.codecogs.com/eq.latex?\\d_2(N)=3.4873+0.0250141N-0.00009823N^2\\d_3(N)=0.80818-0.0051871N+0.00005098N^2-0.00000019N^3\\d_4(N)=2.88606+0.051313N-0.00049243N^2+0.00000188N^3 ]
とのことなので、実証機の測定値の最大と最小の差が母標準偏差の
d_2(100) = 3.4873+0.0250141*100-0.00009823*100^2 ≒ 5.00641
倍であるものと仮定すると母標準偏差は
(最大-最小)/5.00641
程度であると推定できる。従って
Ge半導体検出器 母標準偏差の推定値
-------------- ------------------
18.9 3.87503221
31.2 5.02955211
50.1 4.23457128
67.7 4.86576209
77.7 4.84978258
96.8 5.46299644
112.7 5.72266355
-------------- ------------------
(続く)
|
|
>>5 (続き)
図「実証機の母標準偏差の推定値」
[ http://chart.apis.google.com/chart?hl=ja&cht=lxy&chs=500x500&chg=9.09091,33.33333,2,2&chtt=%E5%AE%9F%E8%A8%BC%E6%A9%9F%E3%81%AE%E6%AF%8D%E6%A8%99%E6%BA%96%E5%81%8F%E5%B7%AE%E3%81%AE%E6%8E%A8%E5%AE%9A%E5%80%A4|(%E5%8D%98%E4%BD%8D:+Bq%2Fkg)&chts=0000FF,20&chxt=x,x,y,y&chxr=0,10,120,10|2,3,6,1&chxp=1,50|3,50&chxl=1:|%E7%8E%84%E7%B1%B3%E3%81%AE%E3%82%BB%E3%82%B7%E3%82%A6%E3%83%A0%E6%BF%83%E5%BA%A6|3:|%E6%8E%A8%E5%AE%9A%E5%80%A4&chxs=1,0000FF,15,0|3,0000FF,15,0&chds=10,120,3,6,10,120,0,130,10,120,0,130&chd=t:18.9,31.2,50.1,67.7,77.7,96.8,112.7|-1|-1|27.6,45.82,60.90,81.10,90.49,112.52,124.40|-1|8.2,20.64,39.70,56.74,66.21,85.17,95.75&chfd=1,ymax,3;ymin,5,(ymax-ymin)/5.00641&chls=1|0|0&chm=o,,0,-1,4|N*f,,0,-1,10 ]
となるが、図「実証試験結果 ゲルマニウム検出器との比較」には「100回測定でも測定値差は、最大で15Bq/kg」とあるので、母標準偏差は最大で
(15*2)/5.00641 ≒ 5.99231785
程度である。
■ 実証機の平均値はGe半導体検出器より約 0.2Bq/kg 少ない。
Ge半導体検出器の測定値を X 軸、実証機の平均値を Y 軸とし
(続く)
|
|
つまり、、 福島産を、許容すると、、 死んじゃうぞー♪ぷっ 食べねーよー♪ばか うさぎ♂ <反抗期です♪w
[18初期非表示理由]:担当:反原発を装い、原発を推進して日本を今日の大破局に追いやった自民党=利権官僚政府と原子力ムラには批判も非難もせず口を開けば『小出がー』『松本ガー』『共産党がー』とやって利権者以外を誹謗中傷するコメント多数のため全部処理http://www.asyura2.com/16/genpatu46/msg/413.html#c82
|
|
>>6 (続き)
b = (n*(Σx_i*y_i)-(Σx_i)*(Σy_i))/(n*(Σx_i^2)-(Σx_i)^2)
a = ((Σy_i)-b*(Σx_i))/n
y = a+b*x
[ http://www.codecogs.com/eq.latex?\\b=\frac{n(\sum%20x_iy_i)-(\sum%20x_i)(\sum%20y_i)}{n(\sum%20x_i^2)-(\sum%20x_i)^2}\\a=\frac{(\sum%20y_i)-b(\sum%20x_i)}{n}\\y=a+bx ]
により、回帰直線を求めると
b = (7*(18.9*17.1+31.2*31.64+50.1*49.18+67.7*69.22+77.7*77.26+96.8*97.58+112.7*109.91)-(18.9+31.2+50.1+67.7+77.7+96.8+112.7)*(17.1+31.64+49.18+69.22+77.26+97.58+109.91))/(7*(18.9^2+31.2^2+50.1^2+67.7^2+77.7^2+96.8^2+112.7^2)-(18.9+31.2+50.1+67.7+77.7+96.8+112.7)^2) ≒ 0.995982423
a = ((17.1+31.64+49.18+69.22+77.26+97.58+109.91)-0.995982423*(18.9+31.2+50.1+67.7+77.7+96.8+112.7))/7 ≒ -0.19737153
y ≒ 0.995982423*x-0.19737153
となる。y = x となるのが理想だが、実証機ではGe半導体検出器より約 0.2Bq/kg 少なく測定されている。
(続く)
|
|
>>8 (続き)
図「実証機の測定値に対する回帰直線」
[ http://chart.apis.google.com/chart?hl=ja&cht=lxy&chs=500x500&chg=9.09091,9.09091,2,2&chtt=%E5%AE%9F%E8%A8%BC%E6%A9%9F%E3%81%AE%E6%B8%AC%E5%AE%9A%E5%80%A4%E3%81%AB%E5%AF%BE%E3%81%99%E3%82%8B%E5%9B%9E%E5%B8%B0%E7%9B%B4%E7%B7%9A|(%E5%8D%98%E4%BD%8D:+Bq%2Fkg)&chts=0000FF,20&chxt=x,x,y,y&chxr=0,10,120,10|2,10,120,10&chxp=1,50|3,50&chxl=1:|%E7%8E%84%E7%B1%B3%E3%81%AE%E3%82%BB%E3%82%B7%E3%82%A6%E3%83%A0%E6%BF%83%E5%BA%A6|3:|%E6%B8%AC%E5%AE%9A%E5%80%A4&chxs=1,0000FF,15|3,0000FF,15&chds=10,120,10,120,10,120,10,120&chd=t:18.9,31.2,50.1,67.7,77.7,96.8,112.7|17.1,31.64,49.18,69.22,77.26,97.58,109.91|-1|-1&chfd=2,x,0,x|3,x,0,-0.19737153%2B0.995982423*x&chls=0|1&chm=o,,0,-1,4|N*f,,0,-1,10|@ty%20=%200.995982423%20x%20-%200.19737153,,0,.1:.9,10 ]
■ セシウム濃度の統計誤差
試料のセシウム濃度 (N_sb/t_sb-N_b/t_b)/m は確率変数であり、次の正規分布に従う。(導出は過去にコメントしているので省略)
(続く)
|
|
>>9 (続き)
(N_sb/t_sb-N_b/t_b)/m 〜 N(μ,σ^2)
μ = ρ
σ^2 = ρ/(m*t_sb)+(ν_b/m^2)*(1/t_sb+1/t_b)
[ http://www.codecogs.com/eq.latex?\\\frac{\frac{N_{sb}}{t_{sb}}-\frac{N_b}{t_b}}{m}\sim\mathrm{N}(\mu,\sigma^2)\\\mu=\rho\\\sigma^2=\frac{\rho}{mt_{sb}}+\frac{\nu_b}{m^2}\left(\frac{1}{t_{sb}}+\frac{1}{t_b}\right)
]
ここで
N_sb∈[0,∞): 試料の計数(バックグラウンド込み)[c] (確率変数)
t_sb∈(0,∞): 試料の測定時間(バックグラウンド込み)[s]
N_b∈[0,∞): バックグラウンドの計数[c] (確率変数)
t_b∈(0,∞): バックグラウンドの測定時間[s]
m∈(0,∞): 試料の質量[kg]
N(μ,σ^2): μ、σ^2を母数とする正規分布
μ: 正規分布の平均
σ^2: 正規分布の分散
ρ∈[0,∞): 試料のセシウム濃度の真値[Bq/kg]
ν_b∈[0,∞): バックグラウンドの計数率の真値[cps]
である。母標準偏差 σ が統計誤差であるが σ = 0 ならば ρ = ν_b = 0 となり、正規分布はディラックの δ 関数 δ(x) に一致する。これは測定値が常に 0 である事を意味しているので、検討対象からは外すことにする。σ > 0 の場合は
σ = (α*ρ+β)^(1/2)
α = 1/(m*t_sb)
β = (ν_b/m^2)*(1/t_sb+1/t_b)
[ http://www.codecogs.com/eq.latex?\\\sigma=(\alpha\rho+\beta)^{\frac{1}{2}}\\\alpha=\frac{1}{mt_{sb}}\\\beta=\frac{\nu_b}{m^2}\left(\frac{1}{t_{sb}}+\frac{1}{t_b}\right) ]
とおき
(続く)
|
|
| |
>>10 (続き)
f(ρ) = (s-μ)/σ = (s-ρ)/(α*ρ+β)^(1/2)
[ http://www.codecogs.com/eq.latex?f(\rho)=\frac{s-\mu}{\sigma}=\frac{s-\rho}{(\alpha\rho+\beta)^{\frac{1}{2}}} ]
と定めれば
f'(ρ) = -((α/2)*(s+ρ)+β)/(α*ρ+β)^(3/2) f(ρ_2) である。これは「セシウム濃度の真値がスクリーニングレベル以上である試料を測定した時に、その測定値がスクリーニングレベル以下になる確率は、試料のセシウム濃度の真値が大きいほど小さくなる」事を示している。
■ 実証機が基準値を超えた試料を安全であると判定(偽陰性)する確率は、スクリーニングレベルが 76Bq/kg 以下ならばほとんど 0 である。
セシウム濃度の統計誤差に関しては
「セシウム濃度の真値がスクリーニングレベル以上である試料を測定した時に、その測定値がスクリーニングレベル以下となる確率は、試料のセシウム濃度の真値が大きいほど小さくなる」
が、系統誤差を含めた場合にこの条件が満たされるかどうかはわからない。しかし、この条件が満たされないとスクリーニング自体が成立しないので、系統誤差を含めてこの条件が満たされているものと仮定する。
従って、偽陰性の確率が最大になるのは試料のセシウム濃度の真値が基準値 100Bq/kg に等しい時であり、母標準偏差の最大値の推定値 5.99231785 を用いてこの時の偽陰性の確率の最大値を計算すると
(続く)
|
|
>>11 (続き)
スクリーニングレベル 偽陰性の確率の最大値
-------------------- --------------------
50Bq/kg 3.59044E-17
60Bq/kg 1.23436E-11
70Bq/kg 2.77273E-07
76Bq/kg 3.0992E-05
80Bq/kg 0.000422516
90Bq/kg 0.0475782
100Bq/kg 0.5
-------------------- --------------------
(続く)
|
|
>>12 (続き)
図「偽陰性の最大確率」
[ http://chart.apis.google.com/chart?hl=ja&cht=lc&chs=500x500&chg=20,16.66667,2,2&chtt=%E5%81%BD%E9%99%B0%E6%80%A7%E3%81%AE%E6%9C%80%E5%A4%A7%E7%A2%BA%E7%8E%87&chts=0000FF,20&chxt=x,x,y,y&chxr=0,50,100,10|2,0,.6,0.1&chxp=1,50|3,50&chxl=1:|%E3%82%B9%E3%82%AF%E3%83%AA%E3%83%BC%E3%83%8B%E3%83%B3%E3%82%B0%E3%83%AC%E3%83%99%E3%83%AB+(Bq%2Fkg)|3:|%E6%9C%80%E5%A4%A7%E7%A2%BA%E7%8E%87&chxs=1,0000FF,15,0|3,0000FF,15,0&chds=0,.6&chd=t:-1&chfd=0,x,50,100,1,.5-sign((100-x)/5.99231785)*(.5-.5/(1%2Babs((100-x)/5.99231785)*(.049867347%2Babs((100-x)/5.99231785)*(.0211410061%2Babs((100-x)/5.99231785)*(.0032776263%2Babs((100-x)/5.99231785)*(3.80036E-5%2Babs((100-x)/5.99231785)*(4.88906E-5%2Babs((100-x)/5.99231785)*5.383E-6))))))^16)&chm=o,,0,26,4|N*f6,,0,26,12,,l:4:4|@a,,0,.55:.05,5|@t76%20Bq/kg,,0,.55:.1,10 ]
となる。スクリーニングレベル 76Bq/kg で基準値 100Bq/kg を僅かに超過した試料 32266 点を実証機で測定すると、そのうちの 1 点だけが誤って安全と判定されるくらいに精度が高いのである。
(了)
|
|
よく読んでませんが、 コンベアー検知器は? 児玉龍彦の、発案で、知人の、島津製作所が、製作したと思います。 ガーネット半導体で、優秀だそうです。 動画では、検知器の、通過時間は? たった、3秒と思いますw 30kg なお、実証実験は? 自分の、島津製作所だってさー♪ばか うさぎ♂ 実証実験は? 産総研や、外国の、三者機関が常識と思うけど?ぷっ♪
[18初期非表示理由]:担当:反原発を装い、原発を推進して日本を今日の大破局に追いやった自民党=利権官僚政府と原子力ムラには批判も非難もせず口を開けば『小出がー』『松本ガー』『共産党がー』とやって利権者以外を誹謗中傷するコメント多数のため全部処理http://www.asyura2.com/16/genpatu46/msg/413.html#c82
|
|
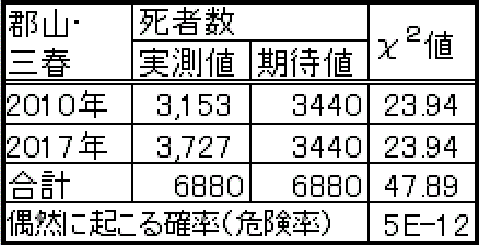
ついでに「表―2」の出鱈目カイ2乗検定についても触れておく。
死者数
-------------
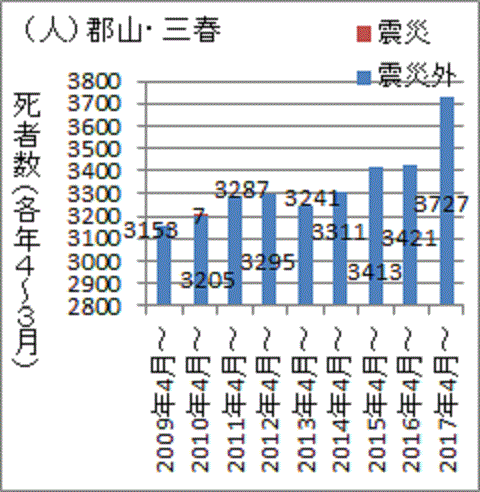
郡山・三春 実測値 期待値 χ^2値
---------- ------ ------ ------
2010年 3153 3440 23.94
2017年 3727 3440 23.94
合計 6880 6880 47.89
------------------------ ------
偶然に起こる確率(危険率) 5E-12
------------------------ ------
の 2010 年の χ^2 値は
(3153-3440)^2/3440 ≒ 23.9444767
2017 年の χ^2 値は
(3727-3440)^2/3440 ≒ 23.9444767
と計算してこれらの合計を求めているわけだが、これは「歪みのないコインを 6880 回投げた時に表(裏)が 0〜3153 回、または 3727〜6880 回出る確率」の計算と同じ(このこと自体が失笑もの)で、そもそもカイ2乗検定を使うまでもない。
平均 6880*0.5、分散 6880*0.5*(1-0.5) の正規分布の確率密度の -∞ から 3153 までの積分と 3727 から ∞ までの積分を加えるだけの話だ。実際にはもっと簡単で、標準正規分布の密度関数を
(3727-6880*0.5)/√(6880*0.5*(1-0.5)) ≒ 6.9201845
から ∞ まで積分して倍にすればいい。なので 標準正規得点 6.9201845 の上側確率 2.25528E-12 を倍にした 4.51056E-12 が答になる。[ http://aoki2.si.gunma-u.ac.jp/CGI-BIN/gxp.html ]
この答を見て「なんだ『めげ猫』の結果と同じじゃねーか」と思う人がいるかもしれなが、「コインの確率」の例えを見て疑問を持たないような人は論外だ。
(続く)
|
|
>>15 (続き)
まあ、強いてやるならこの場合は χ^2 統計量を
A B | A+B
C D | C+D
---------+---------
A+C B+D | A+B+C+D
A: 3153
B: 郡山・三春の2010年の人口 - 3153
C: 3727
D: 郡山・三春の2017年の人口 - 3727
χ^2 = (A-(A+C)*(A+B)/(A+B+C+D))^2/((A+C)*(A+B)/(A+B+C+D))
+ (B-(B+D)*(A+B)/(A+B+C+D))^2/((B+D)*(A+B)/(A+B+C+D))
+ (C-(A+C)*(C+D)/(A+B+C+D))^2/((A+C)*(C+D)/(A+B+C+D))
+ (D-(B+D)*(C+D)/(A+B+C+D))^2/((B+D)*(C+D)/(A+B+C+D))
と計算し、自由度 1 (=(2-1)*(2-1)) のカイ2乗分布で P 値を求めることになる。しかも事前に年齢調整をする必要があり、更に悪いことには 2010 年と 2017 年の郡山・三春の住民に関する統計値は独立ではない(この間、ずっとここに住んでいる人が間違いなくいるから)。独立でない場合、カイ2乗検定は使えない。
俺が「めげ猫」の死亡者数のカイ2乗検定を出鱈目だというのはこういう理由だ。
この種の死亡者数に関する判断材料は各地の行政が出している「標準化死亡比」のデータを見るのがベストで、おそらく専門家でない一般の人には唯一の方法だろう。
(了)
|
|
わっはっはー♪w (=^・^=)ちゃん、、負けー♪ぷっ がんばれよ!w 応援♪ まぁ、天気図、海流、水理、FEM、プログラム、、大変だー♪ まぁ、行列、マトリックス? 多元連立、微分方程式かなー♪? うさぎ♂ <ちょっと、経験者w 麦しよー♪
[18初期非表示理由]:担当:反原発を装い、原発を推進して日本を今日の大破局に追いやった自民党=利権官僚政府と原子力ムラには批判も非難もせず口を開けば『小出がー』『松本ガー』『共産党がー』とやって利権者以外を誹謗中傷するコメント多数のため全部処理http://www.asyura2.com/16/genpatu46/msg/413.html#c82
|
|
>>17
おい、茶色のうさぎ、喜べ。
汁がツイッターのアカウント s01aFkwkqTyLDCT ( https://twitter.com/s01aFkwkqTyLDCT/ ) を BOT に乗っ取られたぞ。いかがわしいサイトでも見てたんだろうwww
緊急用の q16IVZIgv9xwrD4 ( https://twitter.com/q16IVZIgv9xwrD4/ ) から発信しだした汁だが、フォロワー 0 人に。残念無念www
2度と阿修羅に戻ってくるなよ、汁www
|
|
まぁ、、 変動? 誤差? 5%? 3%? 以下、以上は、、異常だー♪ 中学生うさぎ♂ y = a.x <1次関数グラフ
[18初期非表示理由]:担当:反原発を装い、原発を推進して日本を今日の大破局に追いやった自民党=利権官僚政府と原子力ムラには批判も非難もせず口を開けば『小出がー』『松本ガー』『共産党がー』とやって利権者以外を誹謗中傷するコメント多数のため全部処理http://www.asyura2.com/16/genpatu46/msg/413.html#c82
|
|
うむー♪ 麦が、うまい♪ www うさぎ♂ 小出はー? 自殺しろ! ぺっ♪
[18初期非表示理由]:担当:反原発を装い、原発を推進して日本を今日の大破局に追いやった自民党=利権官僚政府と原子力ムラには批判も非難もせず口を開けば『小出がー』『松本ガー』『共産党がー』とやって利権者以外を誹謗中傷するコメント多数のため全部処理http://www.asyura2.com/16/genpatu46/msg/413.html#c82
|
|


 スパムメールの中から見つけ出すためにメールのタイトルには必ず「阿修羅さんへ」と記述してください。
スパムメールの中から見つけ出すためにメールのタイトルには必ず「阿修羅さんへ」と記述してください。