http://www.asyura2.com/14/iryo4/msg/672.html
| Tweet |
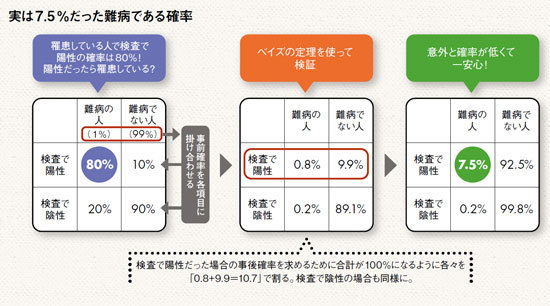
実は7.5％だった難病である確率
で「人口の1％」の難病の疑いが！ 実際に病気になる確率は？
http://zasshi.news.yahoo.co.jp/article?a=20151011-00016343-president-bus_all
プレジデント 10月11日(日)16時15分配信
健康診断は、年をとるにつれて不安が増すもの。自分の検査結果を見て、一喜一憂する読者の方も多いのではないだろうか。今回は、そんな健康診断の数字について、ある難病に罹る確率を例に考えてみたい。
この難病に罹患する人は、人口の1％で、99％の人は罹らない。病気に罹っているか否かを調べるために検査を受けたとき、実際に罹患している人が陽性になる確率は80％、罹患しているものの陰性となる確率は20％だ。もしもあなたが陽性だったとしても、早合点してはいけない。
どうしてかは「ベイズの定理」という確率論で説明できる。実は図左の数字には、この病気に罹る人が人口の1％である(99％の人は罹らない)確率が加味されていない。この1％と99％という最初の確率のことをベイズの定理では「事前確率」と呼び、この事前確率を掛け合わせる必要があるのだ。
そして、掛け合わせた結果が中央図だ。ところが今度は、検査で陽性の人が病気に罹患している確率が0.8％、罹患していない確率は9.9％になってしまった。本来なら合計は100％のはず。そこでベイズの定理では、この2つの合計を100％ にするため、「0.8+9.9=10.7」で各々を割る。そして出た確率を「事後確率」といい、その結果が図右である。
つまり、検査で陽性だったあなたが、実際に病気に罹っている可能性は7.5％ということになる。少しは安心できたはずである。
さて、今回の難病の検査の例でわかったことは何か。それは最初の事前確率の後に、さまざまな変化(情報量の増加)が起き、事後確率が計算できるということだ。つまり、確率は情報量の変動によって常に変化するのだ。
実はベイズの定理は、普段の生活でもさまざまな形で存在する。おもしろい例が競馬だ。10頭の馬が出走する場合、どの馬が勝つかの事前確率は10分の1だ。しかし、馬券を買う人はみな自分なりの情報、たとえば馬の血統や年齢、過去の成績などを持っている。これは複雑すぎて計算できないが、そうした情報を加味して、本人なりの事後確率を弾き出しているのだ。
ビジネスにおいても無意識のうちに、このような複雑な確率計算をしている。次に打つべき手は何かを考えるとき、情報量が多いほどより正確な確率計算ができる。当然、仕事の成功率も高まるはずである。
サイエンス作家 竹内 薫 構成＝田之上 信
投稿コメント全ログ コメント即時配信 スレ建て依頼 削除コメント確認方法
スパムメールの中から見つけ出すためにメールのタイトルには必ず「阿修羅さんへ」と記述してください。すべてのページの引用、転載、リンクを許可します。確認メールは不要です。引用元リンクを表示してください。