消費増税の起爆装置「経済成長率3％」の落とし穴
稼働率50％未満の日本経済のGDPは奈落の底へ

　アメリカ海洋大気局という行政機関が、YouTubeで「Touring the Ocean Bottom」という動画を公開している。「海底探検旅行」といったところか。地球上の海水をすべて取り除いた場合に現われる海底を、3次元映像で描いたものだ。

　マリアナ海溝が最も深く、10.9kmと表示されていた。エベレスト山を引っ繰り返しても、まだ余裕がある。客船タイタニック号が「永眠する深さfinal resting depth：3.8km」も表示されていた。富士山を上下反転させた距離である。

　筆者は栃木県小山市在住なので、海というものを知らない。北の男体山と東の筑波山で、地球の起伏を理解する程度。これからの季節、西の赤城山からは空っ風が吹きすさぶ。海底がどうなっているのかなど想像したことがない。

　だからであろう。「海底探検旅行」の動画には思わず、のけぞってしまった。ときに視点を変えるのはいいものだ。

　ということで今回は、国内総生産GDPや国民所得NIというマクロ経済指標を、「管理会計の視点」から眺めたらどうなるか、ということを紹介しよう。経済学者やエコノミストたちの「立ち位置」からは見ることができない「日本経済の姿」を、水面下に潜って調べてみようという試みだ。

消費税増税の起爆装置
「名目3％の経済成長率」

　通常、個人の生活に、マクロ経済が関わることはない。新聞の経済欄や経済雑誌などで、国内総生産（GDP：Gross Domestic Product）や国民所得（NI：National Income）の文字や数値が躍ることはあっても、「どこの世界の話だ？」である。

　ところが、2012年8月に公布された消費税法附則18条と地方交付税法附則19条を参照すると、「名目の経済成長率で3パーセント程度かつ実質の経済成長率で2パーセント程度を目指した望ましい経済成長の在り方」が明記されている。

　この条文の根拠が、首相官邸ウェブサイトに掲げられている「日本再生戦略」にあるのはいうまでもない。当該サイトの中段よりやや下のところにある「デフレからの脱却」に、「名目成長率で3％程度、実質成長率で2％程度の、望ましい経済成長につなげてきます」とある。

　すなわち、経済成長率が名目で3％、実質で2％を超えたとき、これが起爆装置となって、消費税率は引き上げられる。個人の生活に「いよいよマクロ経済も関わってきたか」と腰を据えて取りかからなければならない時代になったのだ。

　今後、買い物や食事をするとき、「長いものには巻かれろ」で消費税を黙って支払ったりしてはいけない。財布から現金を取り出すとき、「ところで、ニッポンの経済成長率はどうなっているの？」と疑問を持つようにしたいものだ。

　ところで、消費税法では経済成長率と書かれてあるが、内閣府「国民経済計算（GDP統計）」では「GDP成長率」の表現が用いられている。以下では、GDP成長率のほうを用いる。

　GDP成長率とは、国内総生産GDPの変化率をいう。名目値から、物価の上昇や下落分を取り除いたものが、実質値になる（内閣府FAQ）。

「国民経済計算（GDP統計）」の中段に、GDP成長率の四半期ベースや年次ベースの速報値が掲載されている。消費税率が引き上げられるときは、真っ先にチェックしたいサイトだ。

　GDP成長率は、地上に立つ者が見上げる「高さ」である。2％や3％といった値の「小ささ」がクセモノだ。値が小さいと、人は痛痒を感じないものである。

　そこで視点を変えてみる。国内総生産GDPの水面下は、どうなっているのであろうか。アメリカ海洋大気局を真似て、「GDP海底探検旅行」をしてみよう。

SNA産業連関表を、
大胆にも引っ張り出す

　準備作業として、「国民経済計算（GDP統計）」の奥にある「SNA産業連関表」というサイトにアクセスしてみた。そこに掲載されているものを次の〔図表 1〕に掲げる。

拡大画像表示

　SNA産業連関表は、その序文にも書かれてあるように「生産面からのデータから導出」されるものだ。平成11年以前のデータは、同サイトの下のほうに掲載されている。

 〔図表 1〕にある「3　支出＝付加価値」を、ここでは国内総生産GDPと解釈する。総務省統計局「第3章　国民経済計算」を参照すると、「国内総生産（GDP）は，国（地域）内の生産活動による財貨・サービスの産出から原材料などの中間投入を控除した付加価値の総計である」と定義されているからだ。縦割り行政とはいえ、内閣府と総務省とでその解釈が異なることはないであろう。

　したがって、〔図表 1〕右端にある「支出＝付加価値466兆0245億円」は、平成21年（2009年）の国内総生産GDPを表わす。さらに、同年の国民所得NIは、331兆3205億円と推計される。この推計方法は、「第3章　国民経済計算」の「3-10　国民所得」を参照のこと。

 〔図表 1〕の「3　支出＝付加価値」の行において、（　）で示されている百分率は、名目GDP成長率になる。

　消費税法附則18条や地方交付税法附則19条に示されている名目GDP成長率は「3％」であって、「3.0％」とされていない。「2.5％」なら四捨五入して、「消費税率を引き上げることにする」といった詭弁を、政府が弄する可能性がある。

　いや、〔図表 1〕にある「3　支出＝付加価値」の金額自体、いかようにでも操作できる。内閣府以外の外部の第三者には、検証ができないのだから。これは杞憂か。国民として、政府が提示する数字のカラクリには用心したい。

SNA産業連関表と
管理会計の符合

　こうした「初級マクロ経済学」を展開している中で、筆者は面白い符合に気がついた。SNA産業連関表の項目が、管理会計の項目と対応させることができる点だ。その概要が、次の〔図表 2〕である。なお、〔図表 1〕の下から3行目にある項目を、〔図表 2〕では「税金・補助金」と読み替えている。

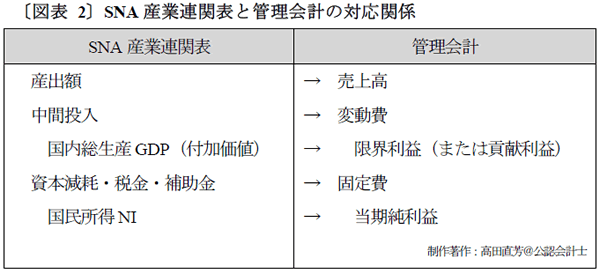
 〔図表 2〕右側にある変動費は、材料費や外注費などから構成される。これは企業の立場からすれば、中間投入だ。

　限界利益（または貢献利益）の正体が「付加価値」であることは、第93回コラム（ＮＥＣ＆富士通編）の〔図表10〕で説明した。拙著『ほんとうにわかる管理会計＆戦略会計』では、「事業付加価値」と称していることを紹介させていただく。

 〔図表 2〕左側のSNA産業連関表に計上されている「資本減耗・税金・補助金」は、固定費とみなすことができる。以上より、国民所得NIは、当期純利益に対応することがわかる。

　国内総生産GDPの正体が、管理会計でいう限界利益（または貢献利益）に対応するとは、誰も想像しなかった展開であろう。暴論といわれそうだ。

　それは違う。経済学を専門とする人々は管理会計の世界に興味はないし、会計学を専門とする人々はSNA産業連関表に関心を持たない。互いに興味がなければ、互いを関連づけようという発想は生まれない。門外漢は口を挟むな、という風潮もある。ただそれだけの話だ。

　さて、本連載を読み続けてこられた読者であれば、この先の展開が読めるはず。その通り。マクロ経済学に、タカダ式操業度分析を適用するのである。欧米の経済学の教科書を翻訳しただけの経済分析とは一味異なるものを、以下で展開していこう。

単利計算構造と
複利計算構造の確執

　タカダ式操業度分析は当初、SCP分析（Sale Cost and Profit Analysis）と称していた。現在はSCP分析よりも、タカダ式操業度分析の名称のほうをメインにしている。その基本命題は、コストやキャッシュは「日々複利の連鎖構造を内蔵」し、企業は「日々複利的な成長過程を遂げるもの」とするところにある。

　企業実務を観察していると、昨日稼いだキャッシュは今日へ再投資され、今日稼いだキャッシュは明日へ再投資されていることがわかる。日々行なわれる再投資はすなわち、「日々複利運用」なのである。それがタカダ式操業度分析を展開するにあたっての基本命題だ。

　第94回コラム（パナソニック編）では、自己資本も「日々複利運用」されるものである、という命題を提起し、自己資本利益率ROEや株価純資産倍率PBRが、複利計算構造を内蔵していることを説明した。

　ところが、管理会計や経営分析などの世界では通常、筆者のように「日々複利」の命題を語らない。CVP分析（損益分岐点分析＆限界利益分析）で代表されるように、1次関数を利用した単利計算構造が絶対的な地位を占める。その日に稼いだキャッシュを翌日に再投資することなく、金庫に死蔵する。それが、筆者以外の人々が説く管理会計論であり経営分析論だ。

　視覚的な違いで説明しよう。次の〔図表 3〕は、世にある書籍や情報システムなどのすべてで必ず見かけるものだ。故に、これを絶対的通説という。

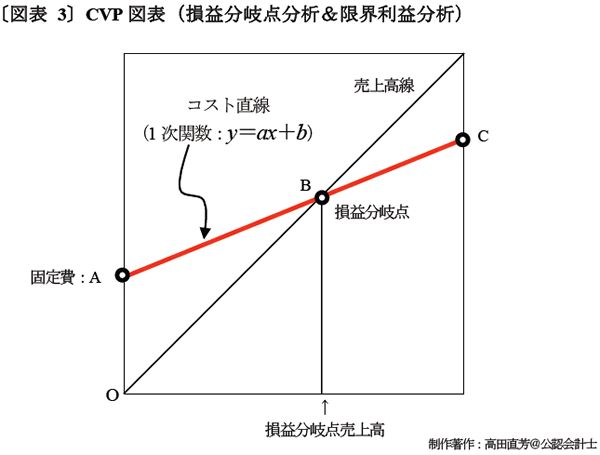
 〔図表 3〕では、縦軸上の点Aから、損益分岐点Bを経由して、右端の点Cまで赤色の直線が描かれている。これが、絶対的通説が描く「コスト直線」だ。その形状は〔図表 3〕で示しているように、1次関数で描かれる。

　次の〔図表 4〕は、タカダ式操業度分析が描く「コスト曲線」だ。

　タカダ式操業度分析は日々複利を仮定するため、数学的には複利関数を使用する。ただし、預金利息の計算や、ディスカウント・キャッシュフローDCF法などで用いられる複利の式をそのまま用いたのでは、微分積分への応用が利かない。

　その近似値として、タカダ式操業度分析では「自然対数の底ｅ」を用いた指数関数を使う。これもまた「複利」を表わすことは、高校のときに習ったはずだ。「自然対数の底ｅ」は、微分積分への応用がきく優れものである。

 〔図表 4〕では、その指数関数を表示している。この関数に基づいてコスト「曲線」は、点D → 点E → 点F → 点G → 点H → 点Jに沿った青色の形状を描く。

日本経済は
複利構造を内蔵している

　日本経済は果たして、〔図表 3〕の1次関数なのか、〔図表 4〕の指数関数なのか。それを確かめるために描いたのが、次の〔図表 5〕である。

 〔図表 5〕は、〔図表 1〕のSNA産業連関表に基づき、1995年（平成7年）から2009年（平成21年）までの「産出額」と「中間投入・資本減耗・税金・補助金」の関係を散布させたものだ。横軸の「産出額」は〔図表 2〕の「売上高」に相当し、縦軸の「中間投入・資本減耗・税金・補助金」は「変動費＋固定費」に相当する。

 〔図表 5〕はどう見ても、〔図表 4〕において青色で描いた指数関数の形状を描いている。日本というマクロ経済も、日々複利的な計算構造を内蔵しているということだ。

 〔図表 5〕では、161兆円を含んだ指数関数を表示している。これは、〔図表 4〕にある点D（基準固定費）が161兆円であることを表わしている。指数関数を用いて基準固定費などを求める方法を、拙著『高田直芳の実践会計講座／戦略ファイナンス』や『会計＆ファイナンスのための数学入門』では「指数関数法による固変分解」と称している。

　固変(こへん)分解とは固定費と変動費に分解する方法をいう。古今東西の会計学や経済学の書籍や学術論文を調べてみても、筆者の書籍以外で「指数関数法による固変分解」を唱えているものは存在しない。筆者オリジナルの方法だ。

　なお、タカダ式操業度分析には、「対数関数法による固変分解」というのもある。これは第89回コラム（シャープ＆ルネサスエレクトロニクス編）の〔図表6〕で紹介した。

マクロ経済学は
2次関数・3次関数の世界

 〔図表 1〕のSNA産業連関表の「13　資本減耗」と「14　税金・補助金」を合わせた平均を求めると、137兆円。これも固定費を構成する。

　資本減耗などの科目によって固定費137兆円を求める方法を、「勘定科目法による固変分解」という。会計の分野では、古くから採用されてきた伝統的な方法だ。

「指数関数法による固変分解」によると、固定費は161兆円。「勘定科目法による固変分解」によると、固定費は137兆円。前者のほうが24兆円も多い。

　その理由は、「指数関数法による固変分解」が、SNA産業連関表の「2　中間投入」にある固定費部分も炙り出すからだ。それはまた、伝統的な管理会計論などが説く「勘定科目法による固変分解」は、1次関数の単利計算構造を採用するが故に、「固定費を過小評価する」という問題を抱えている点に注意してほしい。

　ところで、なぜ、〔図表 5〕は、指数関数（複利関数）の形状を描くのだろうか。その理由は簡単だ。SNA産業連関表にある「中間投入」は、産業から産業へと資源が「再投入」されていく。それは「複利の連鎖構造」を成立させるからだ。タカダ式操業度分析は、そう解釈する。

　経済学者やエコノミストたちは〔図表 5〕を見て、2次関数や3次関数の曲線を思い浮かべるであろう。なぜなら、経済学の教科書は、コスト曲線（費用曲線）を描くにあたって、2次関数や3次関数を用いているからだ（2次関数についてヴァリアン『入門ミクロ経済学』第21章、3次関数についてスティグリッツ『ミクロ経済学』第4章を参照）。

　アメリカの著名な経済学者といえども、マクロ経済を「日々複利の連鎖構造」や「日々複利的な成長過程」と見立てる思考には至っていない。複利運用された預金利息を、2次関数や3次関数で検算しようというのが、現代経済学なのである。これは明らかに誤りだ。

「経済学が実務に役立たない」と揶揄されるのは、こうした基本構造の誤謬を認識しようとしないからであろう。

　情けない話ではあるが、会計の専門家は全員、〔図表 5〕を見て、右上がりの1次関数を主張する。「勘定科目法による固変分解」は〔図表 6〕で示したように、1次関数とセットになっているからだ。国内外を吹き荒れる国際会計基準IFRSも所詮、単利計算構造を前提としている点に注意してほしい。〔図表 6〕に、相違点をまとめておく。

　2008年11月に、拙著『高田直芳の実践会計講座／戦略ファイナンス』を出版する以前は、〔図表 6〕(1)または(2)の考え方しか存在しなかったことを申し添えておく。

　会計学や経済学の教科書に書かれてある話の多くは、欧米で考案された理論を、日本へ「翻訳輸入」したものばかりだ。損益分岐点しかり、ゲーム理論しかり。翻訳したもので「重箱」を作って、その隅をつつく話の、なんと多いことか。

日本経済に
タカダ式操業度分析を当てはめる

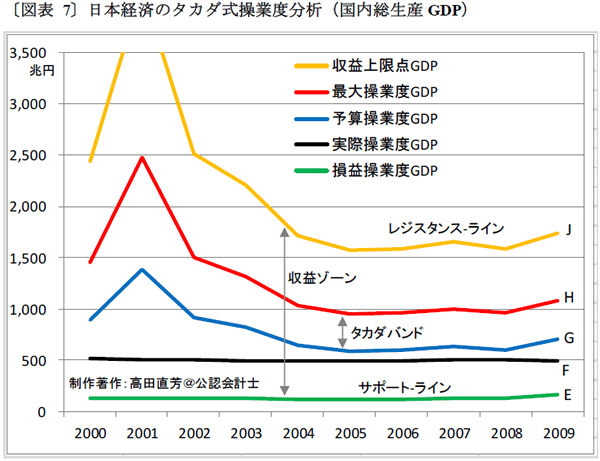
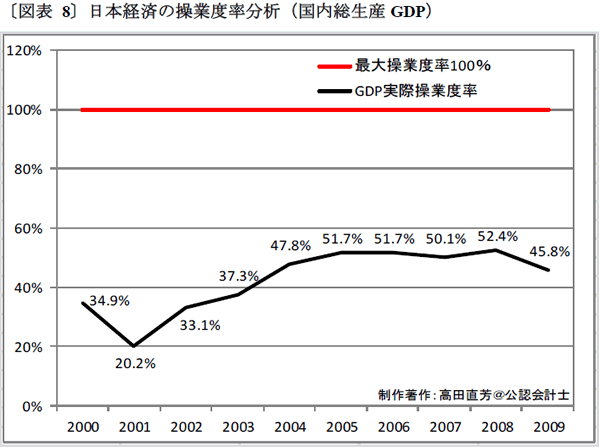
 〔図表 4〕や〔図表 5〕を静態図表という。これらを時系列化した動態図表が、次の〔図表 7〕になる。〔図表 4〕にあった点Eから点Jまでの各記号が、〔図表 7〕の右端に対応している。