http://www.asyura2.com/12/hasan76/msg/628.html
| Tweet |
ノンテクニカルサマリー
労働生産性におけるスケーリング則
執筆者 藤原 義久 (兵庫県立大学)
青山 秀明 (ファカルティフェロー)
Mauro GALLEGATI (Polytechnic University of Marche, Italy)
研究プロジェクト 中小企業のダイナミクス・環境エネルギー・成長
このノンテクニカルサマリーは、分析結果を踏まえつつ、政策的含意を中心に大胆に記述したもので、DPの一部分ではありません。分析内容の詳細はDP本文をお読みください。また、ここに述べられている見解は執筆者個人の責任で発表するものであり、（独）経済産業研究所としての見解を示すものではありません。
新しい産業政策プログラム (第三期：2011〜2015年度)
「中小企業のダイナミクス・環境エネルギー・成長」プロジェクト
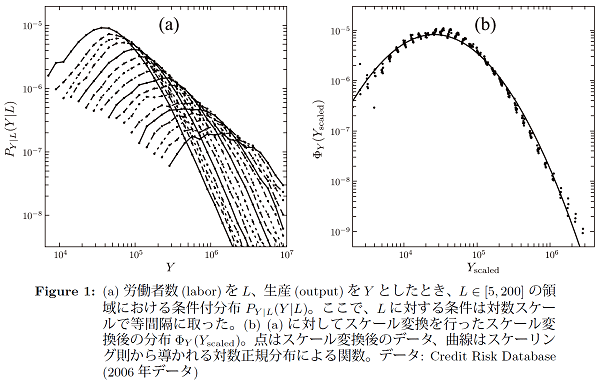
企業の成長とゆらぎの実態を実証的に把握するには、中小企業を含む大規模な企業データを用いて、労働と生産性のダイナミクスを理解することが有益である。特に、労働生産性、生産、労働者の平衡状態での分布がもつ統計的性質はダイナミクスを理解するための鍵である。本研究においては、中小企業の大きな割合をカバーする100万社規模の大規模データを用いて、生産(output)、労働(labor)、労働生産性(labor productivity)に関するばらつき(dispersion)、あるいは分布(distribution)を解析した。
解析の結果、特に生産と労働者数について、それらの周辺分布(marginal distribution)が裾野の長い分布であることに加えて、それらの同時分布(joint distribution) にスケーリング則が潜んでいることを見出した。ここでのスケーリング則は、生産と労働の変数を適切に組み合わせてスケールすることによって、生産または労働についての分布がほとんどの企業を含む広い領域において、普遍的な関数形に従っていることを意味する。そして、生産と労働者数の2つの変数についてスケーリング則が成り立っている(二重スケーリング則)わけである(図を参照)。また、この事実から数学的に示すことができることとして、パラメータの取る値の組合せが一般的なケースでは、周辺分布も同時分布も対数正規(log-normal)分布のタイプに限られること、特殊なケースではそれらがべき(power-law)分布のタイプに限られることが分かった。
これらの特徴的な性質は、それ自体が数学的に興味深く、驚くべきことであるだけでなく、生産および労働者を個々の企業という最もミクロなレベルでみたときに、それらの分布に普遍的な性質が存在していることを意味しており、それらの分布を生成しているダイナミクスを理解する上で、決定的な鍵となりうる。たとえば、対数正規分布やべき分布を生み出す確率過程として、（1）需要制約が存在し生産の総和が一定である系で、需要の個別的なショックによって確率的に生産が変化して、互いに競合してシェアを増減させる過程や、（2）セクター外から新しい企業が参入する過程などを考えることができる。
また、スケーリング則の意義は、生産関数の一般化として捉えることも可能である。すなわち、通常の生産関数の概念においては労働と資本に対する一様な関数によって、生産が決定される。そこでは、コブ・ダグラス型の生産関数に代表されるように、労働をスケールすると生産も一定のスケール倍に変化する。一方、我々の発見は関数ではなく、分布に関するスケール変換についてのものであるので、条件付平均値を含む条件付分布に関する普遍的な生産関数とも解釈することができる。
このようにして生産・労働・生産性が従う基本的なダイナミクスが分かれば、たとえば一定の生産性をもつセクターへの生産要素の追加という政策が生産や労働の再配置にどのような影響を持つのか、などの示唆を得るための方法論が構築できる。これらの性質は法則性というよりは、ダイナミクスのもつパターンを意味しており、異常な状況下では破れたり、特殊なパターンに変化するようなものであるので、たとえば生産性の高いセクターの出現や労働力の配位の変化の検出など、政策的な判断に重要な材料を提供できる可能性がある。
今後、生産・労働・生産性のダイナミクスに関する確率過程のモデル化につなげて、上述の方法論を構築することにより、中小企業政策を考える上で大きな貢献を見込む。
http://www.rieti.go.jp/jp/publications/nts/12e040.html?stylesheet=print
この記事を読んだ人はこんな記事も読んでいます（表示まで20秒程度時間がかかります。）
スパムメールの中から見つけ出すためにメールのタイトルには必ず「阿修羅さんへ」と記述してください。すべてのページの引用、転載、リンクを許可します。確認メールは不要です。引用元リンクを表示してください。
